布隆过滤器
问题场景:给定一组文章 id 列表,如何判断文章 a 的 id 在给定的列表中?
我们很容易使用列表、数组、哈希表等将文章 id 先保存起来,判断重复时,直接遍历数组、列表、根据哈希值判断等。
上面的解决方式,最好的无疑是哈希表。哈希表检索时间复杂度为 O(1),但是这只限于没有发生哈希冲突的情况下,而且数据量一旦比较大,存储占用也会大大增加,会导致检索性能大大下降。
对于数据量较大的场景,如何快速检索元素是否包含在另一个集合中,这就引出今天的主角了「布隆过滤器」。
简介
布隆过滤器(英语:Bloom Filter)是1970年由布隆提出的。它实际上是一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都远远超过一般的算法,缺点是有一定的误识别率和删除困难
简介引用自维基百科,里面有两个概念「二进制向量」,「映射函数」。
二进制向量就是一堆 bit(位) 的集合,bit 我们都知道就是只能表示 0 和 1。其实我们常使用的 int 有 32 位,因此他也可以看做一个二进制向量。
下面是一个简单的示例,每一个空格就代表一个 bit,下面的数字表示它的索引:

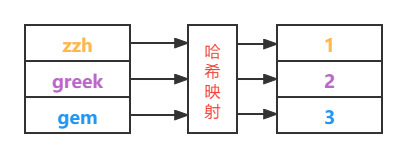
映射函数我们其实很并不陌生。使用过 HashMap 就应该知道,对 key 使用 hashCode 方法,计算哈希值,这个 hashCode 方法就是一个映射函数,一个 key 只能对应一个哈希值。
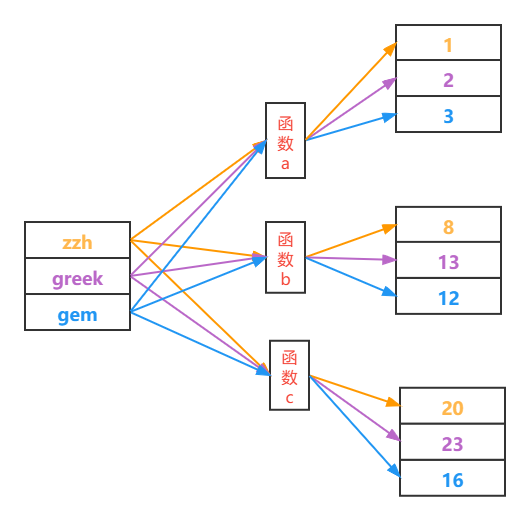
布隆过滤器对一个 key 使用多个映射函数,得到多个值。
哈希函数映射
布隆过滤器中映射函数
原理
了解一些基本概念之后,布隆过滤器的原理就很明了了。
布隆过滤器对于要保存的值使用一系列随机的映射函数,得到二进制向量下标,然后把对应的 bit 置为 1,就是这么简单。
例如,字符串 “zzh”,经过三个随机的映射函数,对应的下标为 2,7,11 因此对应的 bit 为 1。
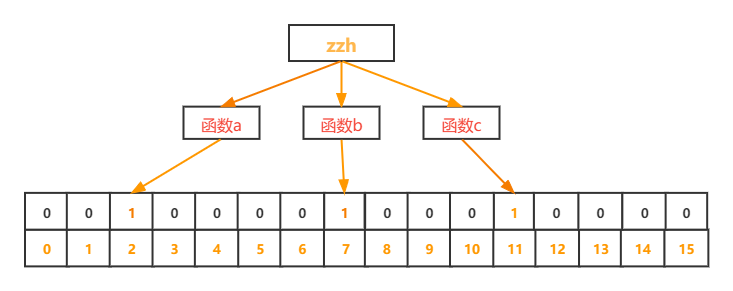
我们可以对要插入到的字符串应用同样的哈希函数,然后看二进制向量里对应的bit 是否全为 1 来判断一个元素是否在集合里。
如果是,则该元素可能在里面,注意是可能。 因为这些位置有可能是由其他元素或者其他元素的组合所引起的,这也就导致了布隆过滤器的误识别率。
如果不是,则表示该元素一定不在集合中。
缺点
我更习惯在介绍一个功能的时候,先把他的缺点说出来,知道缺点的话,后续就可以大胆的应用。
误识别率
插入字符串 “zzh” 得到下标 2、7、11
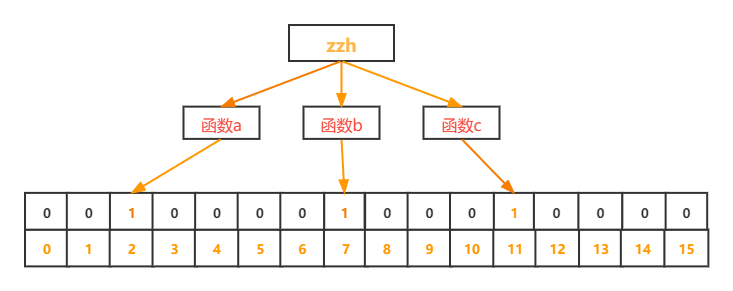
插入字符串 “greek” 得到下标 5、8、9
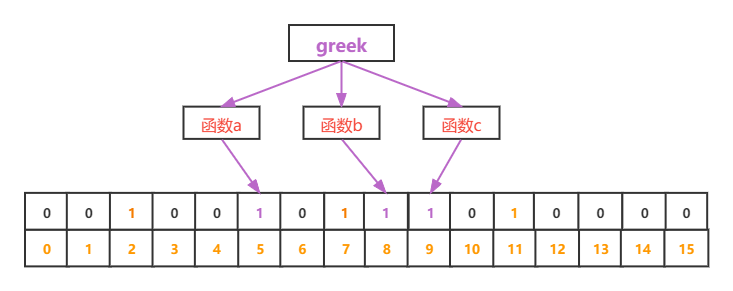
插入字符串 “gem” 得到下标 2、5、8
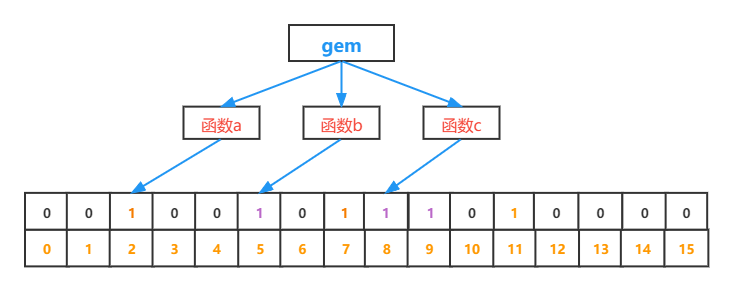
可以看到 “gem” 得到的下标对应的 bit 都已经为 1,但是该字符串并不在集合中,这就是布隆过滤器的误识别率。
删除困难
删除困难的原因和误识别率是如出一辙。例如我们只想把 “gem” 字符串删除,于是把下标为 2、5、8 的 bit 都置为 0,这样的话 “greek” 和 “zzh” 部分数据就被删除了。无法保证删除的下标影响到其他元素,这就是布隆过滤器删除困难的原因。
我们也很容易想到把位数组变成整数数组,每插入一个元素相应的计数器加 1,这样删除元素时将计数器减掉就可以了。但是这样根本不可行,因为连一个元素是否在集合中都无法百分百保证,又何来的把这个元素删除呢?就好比你想能为开源世界大牛,现在却连 GitHub 都无法保证访问一样。
规避手段
识别率和删除困难虽然都是缺点,但都是可以通过一些手段去规避。
假设在布隆过滤器里面有 k 个映射函数, m 个比特, 以及 n 个已插入元素,那么该过滤器误判率近似于:_(1-e-kn/m)k_ 。因此我们可以通过调整映射函数数量和布隆过滤器的大小来降低误判率。
对于应该使用多少个映射函数,国外的一篇博客给了较好的答案,引用部分为原文内容,详情点击
对于给定的 m 和 n ,有一个函数可以帮我们确定最优的 k 值: (m/n)ln(2)
所以可以通过以下的步骤来确定 Bloom filter 的大小:
- 确定 n 的变动范围
- 选定 m 的值
- 计算 k 的最优值
- 对于给定的_n_, m, and _k_计算错误率。如果这个错误率不能接收,那么回到第二步,否则结束
事实上,已经存在许多布隆过滤器变种,他们使用更好的映射函数、支持删除元素、更低的误判率等等。维基百科上记录了 60 多种布隆过滤器的变体。例如:布谷鸟过滤器、布卢姆过滤器、等等,他们相比原始的布隆过滤器往往有更强的特性,详情访问wiki
优点
查询效率和插入效率高,时间复杂度为 O(k) ,k 为映射函数的数量。因为你每次查询或者插入一个元素时,都是通过 k 个函数计算对于的 bit 下标,然后检查对应的 bit 位是否为 1 或者将 bit 位置位 1。
空间效率。布隆过滤器的空间效率取决于你期望的误判率,期望的误判率越小,所需的空间就要更大,因此无法具体量化。我们可以简单的和 HashMap 做个对比。
假设 HashMap 和布隆过滤器都保存字符串 “zzh”,且布隆过滤器使用 3 个映射函数。HashMap 仅保存这个字符串需要 6 个字节,即 48 bit,而布隆过滤器只需要 3 个 bit。
一些应用场景:URL 黑名单判断、垃圾邮箱判断、弱密码检测、比特币钱包同步等等。